MATERIAL BEING ADDED IN NEAR FUTURE
Graphic Deviations
Joint project with
Mark Broom
City University, London.
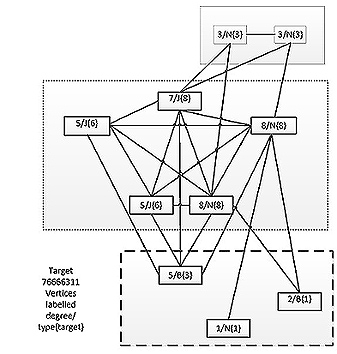 A sequence {x1,x2,x3,........,xn} where x_i is a positive integer is said
to be GRAPHIC if there is a simple graph (i.e. one with no multiple edge
or self-edges) whoes n vertex degrees are precisely x1,x2,.....,xn. Suppose
one has a set of entities associated with each is some integer range, [mi,Mi]
for the ith. This range specifies where the entity would wish to fix its
degree. Suppose there is some simple graph G(t), at time t. A vertex is
selected at random, the ith say. If the degree of i is in [mi,Mi] no change
is made. If i < mi then some j to which i is not currently linked is selected
at random and the edge (i,j) added. If i > Mi then some j to which i is
linked is selected at random and the edge (i,j) deleted. Thus we have a Markov
chain.
A sequence {x1,x2,x3,........,xn} where x_i is a positive integer is said
to be GRAPHIC if there is a simple graph (i.e. one with no multiple edge
or self-edges) whoes n vertex degrees are precisely x1,x2,.....,xn. Suppose
one has a set of entities associated with each is some integer range, [mi,Mi]
for the ith. This range specifies where the entity would wish to fix its
degree. Suppose there is some simple graph G(t), at time t. A vertex is
selected at random, the ith say. If the degree of i is in [mi,Mi] no change
is made. If i < mi then some j to which i is not currently linked is selected
at random and the edge (i,j) added. If i > Mi then some j to which i is
linked is selected at random and the edge (i,j) deleted. Thus we have a Markov
chain.
In our first paper (Broom and Cannings Submitted for publication)we discuss
the basic theory.
Abstract.
We consider an arbitrary sequence of integers
There is growing interest in modeling populations using graph theory
where individuals are represented by vertices and interactions
between pairs by edges. Suppose in some population each individual
has a preferred range for their number of links to other
individuals. There is then, for any graph on those individuals, a
deviation from the preferred values. As individuals adjust their
links according to their preferred range the graph evolves towards
some set of graphs which achieve the minimum possible deviation. The
study of this process raises a new question in graph theory. If we
are given a sequence of $n$ non-negative integers how can we find
the graphs which achieve the minimum deviation from that sequence as
its degrees. This extends the classical problem regarding what
sequence are "graphic", that is can be the degrees of a simple
graph, to issues regarding arbitrary sequences. In this context we
shall demonstrate how a variation on the Havel-Hakimi algorithm can
supply the value of the minimum possible deviation, and how
consideration of the Ruch-Gutman condition and the Ferrer diagram
can yield the complete set of
graphs achieving this minimum.
In our second paper (Broom and Cannings, In Press)we discuss the application of the
model to biological populations via the Markov chain.
Abstract.
Historically most evolutionary models have considered infinite populations with no structure.
Recently more realistic evolutionary models have been developed using evolutionary graph theory,
which considered the evolution of structured populations. The structures involved in these
populations are typically fixed, however, and real populations change their structure over
both long and short time periods. In this paper we consider the dynamics of such a population
structure. The timescales involved are sufficiently short that no individuals are born or die,
but the links between individuals are in a constant state of flux, being actively governed by
the preferences of the members of the population. The process is modelled using a Markov chain
over the possible structures. We find that under the specified process the population evolves
to a closed class of structures, and we show a method to find the stationary distribution on
this class. We also consider some special cases of interest.
Parker's Model
Evolutionary Conflicts with Mutations, 1. Parker's Model.
Parker's Model has no ESS. The object of this project is to study the behaviour
of a population playing Parker's Model with reward V and some set ([0,m] or
{0,1,2,...,m-1}) of possible plays, when individuals playing these strategies
arise through repeated mutation. The aim is to specify the stationary distribution
of such a population.Three papers are in preparation (1) considering general
aspects of the problem, including specification of patterns of dominance and
(2) specifying the stationary distribution in the special class where V is in
(2,4], the strategy set is {0,1,2,....,m-1} and mutations occur infrequently
and uniformly over the possible values.
The Stationary Distribution of a Class of Markov Chains. (2013) Applied Mathematics, 4,
769-773
(3) Suppose there are n possible plays, and there is infrequent mutation with equal rates for all the plays. Then the system will at any time have only two plays one of which will rapidly displace the other. We investigate when every play will be represented in the stationary distribution of the resulting Markov chain. The conditions are related to Catalan numbers and Dcke words.
Combinatorics of Parker's model. Dynamic Games and Applications {To appear}
Best Response Games on Regular Graphs

Joint work with
Richard Southwell
,The Chinese University of Hong Kong.
With the growth of the internet it is becoming increasingly important to understand how
the behaviour of players is affected by the topology of the network
interconnecting them. Many models which involve networks of interacting players have been
proposed and best response games are amongst the simplest. In best
response games each vertex simultaneously updates to employ the best response to their
current surroundings. We concentrate upon trying to understand the
dynamics of best response games on regular graphs with many strategies. When more than
two strategies are present highly complex dynamics can ensue. We focus
upon trying to understand exactly how best response games on regular graphs sample from
the space of possible cellular automata. To understand this issue we
investigate convex divisions in high dimensional space and we prove that almost every
division of (k-1) dimensional space into k convex regions includes a
single point where all regions meet. We then find connections between the convex geometry
of best response games and the theory of alternating circuits on
graphs. Exploiting these unexpected connections allows us to gain an interesting answer
to our question of when cellular automata are best response games.
Best Response Games on Regular Graphs. (2013) Applied Mathematics, 4,
950-962
Trinets
Joint work with
Richard Southwell
and
Jianwei Huang

Exploring the space of substitution systems
Joint work with
Richard Southwell

Southwell R and Cannings C. (2013) Exploring the space of rewrite system. Complex Systems, 22,?-?.
Random Walks and Preferential Attachment
Joint work with
Jonathan Jordan
School of Maths. and Stats.,
University of Sheffield.

Geiringer's Theorem
Joint work with Boris Mitavskiy et al. The University
of Aberystwyth

Pure Nash Equilibria in Co-ordination Games
Joint work with Rob Cannings.
In the congestion game with monotonically decreasing payoffs with
increasing congestion Milchtaich (Games and Economic Behaviour, 13, 111-124 (1996))
proved that there is always a pure Nash equilibrium. We consider the
co-ordination game with increasing payoffs with increasing co-ordination
(see Southwell, ). We prove, by way of counterexamples that, except when there are only
two strategies, there is no guarrantee that a pure Nash equilibrium exist. The model
introduced to provide a counterexample is generalised to provide futher models where
under miopic behaviour we obtains cycles corresponding to the orbits under a cyclic
group action.
(Cannings C and Cannings R, (2013) Absence of pure Nash equilibria in a class
of co-ordination games. (In Press), Statististic, Optimization & Information Computing.
Majority/minority games on graphs.
Joint work with John Haslegrave, SoMaS, University of
Sheffield.
 A sequence {x1,x2,x3,........,xn} where x_i is a positive integer is said
to be GRAPHIC if there is a simple graph (i.e. one with no multiple edge
or self-edges) whoes n vertex degrees are precisely x1,x2,.....,xn. Suppose
one has a set of entities associated with each is some integer range, [mi,Mi]
for the ith. This range specifies where the entity would wish to fix its
degree. Suppose there is some simple graph G(t), at time t. A vertex is
selected at random, the ith say. If the degree of i is in [mi,Mi] no change
is made. If i < mi then some j to which i is not currently linked is selected
at random and the edge (i,j) added. If i > Mi then some j to which i is
linked is selected at random and the edge (i,j) deleted. Thus we have a Markov
chain.
A sequence {x1,x2,x3,........,xn} where x_i is a positive integer is said
to be GRAPHIC if there is a simple graph (i.e. one with no multiple edge
or self-edges) whoes n vertex degrees are precisely x1,x2,.....,xn. Suppose
one has a set of entities associated with each is some integer range, [mi,Mi]
for the ith. This range specifies where the entity would wish to fix its
degree. Suppose there is some simple graph G(t), at time t. A vertex is
selected at random, the ith say. If the degree of i is in [mi,Mi] no change
is made. If i < mi then some j to which i is not currently linked is selected
at random and the edge (i,j) added. If i > Mi then some j to which i is
linked is selected at random and the edge (i,j) deleted. Thus we have a Markov
chain.




